I heard this someplace recently
"The law of bug conservation states that - bugs can neither be created nor destroyed. The total number of bugs remain constant, they only change from one form to another"
Friday, February 25, 2005
Software programming can be humbling
My experience has been that software programming can humble the most experienced programmer. You sometimes need a fresh look at the problem at hand and probably fresh eyes as well to debug a problem. Based on my experience, I am trying to come up with a simple set of rules that might help the programmer with his situation, these rules can be generalized so much so that it almost becomes common sense.
I will keep adding to this list as I get more input from all of you or start thinking clearly.
- Try not too hard to debug a problem, take a break, come back later
- Are you able to explain the problem you are seeing? Can you describe the pattern in which it occurs? Stop looking at the code and try to understand the pattern and possible explanation for it
- Use your friendly debugger or your friendlier console log messages
- Can you narrow down the problem to something simpler
- If you are dealing with numbers - think signed != unsigned
- Are you dealing with garbage data? Garbage data implies faulty pointers or storing more than the capacity
- Do you assert() the code (yourself) frequently enough
- Is this a recently created problem - look at what you changed recently
- Can you simulate what the computer is doing (if you can find the faulty logic in code) on paper or in your mind. If so, there is a good chance of you catching the bug
- Don't solve the same problem twice
I will keep adding to this list as I get more input from all of you or start thinking clearly.
Monday, February 21, 2005
Some articles I recently read
Here are some articles/interviews I recently read and enjoyed
http://www.stlport.org/resources/StepanovUSA.html
http://www.sgi.com/tech/stl/drdobbs-interview.html
http://www.stlport.org/resources/StepanovUSA.html
http://www.sgi.com/tech/stl/drdobbs-interview.html
Wednesday, February 16, 2005
One of the best forewords
I have been reading the forward to "STL Tutorial and Reference Guide" by David R. Musser, Gillmer J. Derge and Atul Saini. The foreword is written by Alexander Stepanov and its one of the best I have read. Great work!
Answer to Fundamentals of Numbers
In the blog post Fundamentals of Numbers, a fundamental question was posted.
Well here is the hint
Take beta=10 and n = 121
121 = 1 * 10^2 + 2 * 10 + 1
Now try the following C based pseudo-code
while (n/beta) {
printf("%d\t", n % beta);
n /= beta;
}
if (n % beta) {
printf("%d\n", n % beta);
}
printf("\n");
It prints out the numbers in opposite order. Get it? No matter what the value of n and beta, we can find a sequence representing n in terms of beta.
This should really be an axiom.
Well here is the hint
Take beta=10 and n = 121
121 = 1 * 10^2 + 2 * 10 + 1
Now try the following C based pseudo-code
while (n/beta) {
printf("%d\t", n % beta);
n /= beta;
}
if (n % beta) {
printf("%d\n", n % beta);
}
printf("\n");
It prints out the numbers in opposite order. Get it? No matter what the value of n and beta, we can find a sequence representing n in terms of beta.
This should really be an axiom.
Thought for the day
Attrition is equivalent to "Gifting talent to your competitors"
Balbir Singh
Lay off's are equivalent to "Ending the mistake that began elsewhere"Balbir Singh
Issues with IE now
My Firefox issues got solved (by using meta tags), thanks to Narasimha. IE does not do a good job of rendering the last post and hence the entire page. As usual, I am working on it.
Monday, February 14, 2005
Fundamentals of Numbers
I am reading Numerical Analysis, a mathematical introduction by Michelle Schatzman. I found some really interesing questions for computer programmers and thought I would post them here followed by their answers in a short while. The questions are quite simple, but you learn more than you expect by answering them
Here is the first one
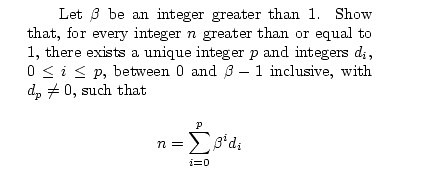
Here is the first one
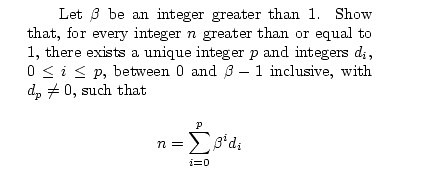
Test MATHML
I frequently use mathematical notation in my daily programming and study. Since some of the notation I use here is mathematical as well, I plan to use MATHML for some of them. But I am unable to add MATHML into my BLOG for now. So, I am stuck with photos that TeX produces, like the one below
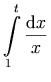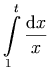
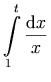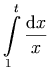
Premier Hockey League
I think one of the best things that happened to hockey is PHL. The finals last night was among the best hockey matches I have seen recently. It was a thrilling encounter with the Sher-e-Jalander requiring to win within 70 minutes. The Sultans won 2-1, sending the home crowd into jubilation.
Sunday, February 13, 2005
Reprints of Low Price Edition (LPE) of Books
One of the biggest disadvantages of Low Price Editions of books is that reprints are merely "reprints". They do not fix any errata as the original editions do. The LPE is only as good as the reprint that the publisher buys from the parent company and does not update it until a new edition is out.
Saturday, February 12, 2005
Efficiency of Autoboxing in Java
I am trying to catch up with the changes in J2SE5.0. One of the feature additions is auto-boxing and auto-unboxing. It's a great feature and simplifies programming, reduces errors, but as well noted it is not efficient. Over use will result in a performance hit. Please see autoboxing notes from SUN for more details. I tried some experiments myself and found that auto-boxing happens each time, no caching is done for auto-boxed or auto-unboxed values. Below is a program and its disassembled output
public class AB4 {
public static void main(String args[])
{
Integer j = new Integer(1000);
int i = j + j + j + j;
int k = j + j;
System.out.println("i is " + i);
System.out.println("j is " + j);
System.out.println("k is " + k);
}
}
Compiled from "AB4.java"
public class AB4 extends java.lang.Object{
public AB4();
Code:
0: aload_0
1: invokespecial #1; //Method java/lang/Object."":()V
4: return
public static void main(java.lang.String[]);
Code:
0: new #2; //class java/lang/Integer
3: dup
4: sipush 1000
7: invokespecial #3; //Method java/lang/Integer."":(I)V
10: astore_1
11: aload_1
12: invokevirtual #4; //Method java/lang/Integer.intValue:()I
15: aload_1
16: invokevirtual #4; //Method java/lang/Integer.intValue:()I
19: iadd
20: aload_1
21: invokevirtual #4; //Method java/lang/Integer.intValue:()I
24: iadd
25: aload_1
26: invokevirtual #4; //Method java/lang/Integer.intValue:()I
29: iadd
30: istore_2
31: aload_1
32: invokevirtual #4; //Method java/lang/Integer.intValue:()I
35: aload_1
36: invokevirtual #4; //Method java/lang/Integer.intValue:()I
39: iadd
40: istore_3
As can be seen, for each occurrence of j, the value is auto-unboxed and then added, could these values not be cached? Maybe, I need to specify a higher level of optimization, but at first glance I could not find specification of the level of optimization.
public class AB4 {
public static void main(String args[])
{
Integer j = new Integer(1000);
int i = j + j + j + j;
int k = j + j;
System.out.println("i is " + i);
System.out.println("j is " + j);
System.out.println("k is " + k);
}
}
Compiled from "AB4.java"
public class AB4 extends java.lang.Object{
public AB4();
Code:
0: aload_0
1: invokespecial #1; //Method java/lang/Object."
4: return
public static void main(java.lang.String[]);
Code:
0: new #2; //class java/lang/Integer
3: dup
4: sipush 1000
7: invokespecial #3; //Method java/lang/Integer."
10: astore_1
11: aload_1
12: invokevirtual #4; //Method java/lang/Integer.intValue:()I
15: aload_1
16: invokevirtual #4; //Method java/lang/Integer.intValue:()I
19: iadd
20: aload_1
21: invokevirtual #4; //Method java/lang/Integer.intValue:()I
24: iadd
25: aload_1
26: invokevirtual #4; //Method java/lang/Integer.intValue:()I
29: iadd
30: istore_2
31: aload_1
32: invokevirtual #4; //Method java/lang/Integer.intValue:()I
35: aload_1
36: invokevirtual #4; //Method java/lang/Integer.intValue:()I
39: iadd
40: istore_3
As can be seen, for each occurrence of j, the value is auto-unboxed and then added, could these values not be cached? Maybe, I need to specify a higher level of optimization, but at first glance I could not find specification of the level of optimization.
Friday, February 11, 2005
Interviews response
My Friend Narasimha spoke about interviewing at http://narasimhagm.blogspot.com/2005/02/interview.html
I find it very interesting, given that I have taken hundreds of interviews and attended quite a few (many times for the kick or out of optimisim or to learn something and/or check my current skills :-))
Here is his list
I find it very interesting, given that I have taken hundreds of interviews and attended quite a few (many times for the kick or out of optimisim or to learn something and/or check my current skills :-))
Here is his list
- Do not get too technical (There is google for this)
- Try to find out if the candidate is passionate about what he has worked on
- Ask some questions which probe his analytical ability
- Ask about academic projects.
- Probe whether he understands some concepts about source control, unit testing
- Ask whether he has uses google :)
- See if the candidate is capable of working independently
- Don't expect him/her to know the obscure details of the language he/she uses for programming. After all a programming language is just a tool
- Check his/her learning ability and flexibility and the willingness to adapt to new technologies
- Check to see if he can tell you the reason for leaving his current job
- Many more to come
Archiving the WEB
I recently found http://www.archive.org/web/web.php. I found it simply amazing, I looked at pages from 1996 and compared them to pages of today, one can clearly see the advancement in web technology. From CGI to technologies of today.
If you do not find your link the in the archives, use http://pages.alexa.com/help/webmasters/index.html#crawl_site to add your URL and the bot will visit your website and start archiving it
I recently found http://www.archive.org/web/web.php. I found it simply amazing, I looked at pages from 1996 and compared them to pages of today, one can clearly see the advancement in web technology. From CGI to technologies of today.
If you do not find your link the in the archives, use http://pages.alexa.com/help/webmasters/index.html#crawl_site to add your URL and the bot will visit your website and start archiving it
Thursday, February 10, 2005
Comments on Big-Oh (O) from CLRS
Section 3.1 of CLRS (Cormen, Leiserson, Rivest, Stein) discuss the Big-Oh notation O. The linear function an + b is O(n2), which is easily verified by taking c = a + |b|. cg(n) is a2n + ba + |b|b + |b|an. At the first glance this seems true if a + b >= n, since O is the worst case, we can use this. In addition, a = b = sqrt(n) also help in making the function O(n2). Please see the plots below
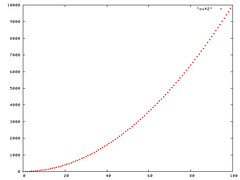
Figure 1: Plot of n2
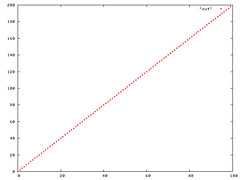
Figure 2: Plot of a = 1,b = n
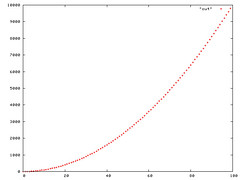
Figure 3: Plot of a = n,b = 1
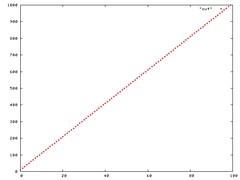
Figure 4: Plot of a = sqrt(n),b = sqrt(n)
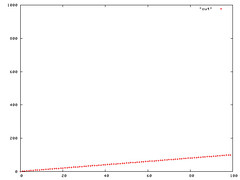
Figure 5:Plot of a = 1,b = 1
I think it is non-trivial to suggest find out that the function is indeed
O(n2). Comments please!
Section 3.1 of CLRS (Cormen, Leiserson, Rivest, Stein) discuss the Big-Oh notation O. The linear function an + b is O(n2), which is easily verified by taking c = a + |b|. cg(n) is a2n + ba + |b|b + |b|an. At the first glance this seems true if a + b >= n, since O is the worst case, we can use this. In addition, a = b = sqrt(n) also help in making the function O(n2). Please see the plots below

Figure 1: Plot of n2

Figure 2: Plot of a = 1,b = n

Figure 3: Plot of a = n,b = 1

Figure 4: Plot of a = sqrt(n),b = sqrt(n)

Figure 5:Plot of a = 1,b = 1
I think it is non-trivial to suggest find out that the function is indeed
O(n2). Comments please!
Expecting Linux Device Drivers, third (3rd) edition

Linux Device Drivers second edition was really good. I think the announcement of the third edition is around the corner. Hopefully the Indian edition or the free online edition will be out soon. Here is a link to some material the authors have put up on the web http://lwn.net/Articles/2.6-kernel-api/ also check out http://www.oreilly.com/catalog/linuxdrive3/

Linux Device Drivers second edition was really good. I think the announcement of the third edition is around the corner. Hopefully the Indian edition or the free online edition will be out soon. Here is a link to some material the authors have put up on the web http://lwn.net/Articles/2.6-kernel-api/ also check out http://www.oreilly.com/catalog/linuxdrive3/
Thursday, February 03, 2005
Probability
My favorite mathematical topic and well covered by the Cormen, et. al book. Chapter 5 of the book covers this topic in depth and explains applications to the "The Hiring Problem". The most interesting thing is ofcourse is the uniformly random permutation and the exercises built around it.
Randomize-in-place(A)
n <- length(A)
for i <- 1 to n
do swap (A[i], A[Random(i, n)])
The example above demonstrates a uniformly random permutation. See the book and if you need help with the exercise solutions, we can discuss it.
The Birthday Paradox implies that with atleast 28 people, we can expect to find atleast one matching pair of birthdays. But, what about the pigeon hole principle? The pigeon hole principle states that we require atleast 366 people to definitely find one pair of matching birthdays.
My favorite mathematical topic and well covered by the Cormen, et. al book. Chapter 5 of the book covers this topic in depth and explains applications to the "The Hiring Problem". The most interesting thing is ofcourse is the uniformly random permutation and the exercises built around it.
Randomize-in-place(A)
n <- length(A)
for i <- 1 to n
do swap (A[i], A[Random(i, n)])
The example above demonstrates a uniformly random permutation. See the book and if you need help with the exercise solutions, we can discuss it.
The Birthday Paradox implies that with atleast 28 people, we can expect to find atleast one matching pair of birthdays. But, what about the pigeon hole principle? The pigeon hole principle states that we require atleast 366 people to definitely find one pair of matching birthdays.
Programmers
Given my software development background and the industry experience I have; I decided to classify programmers. Think of this as a taxonomy, I plan to grow this list as time progresses. A programmer could fall into several categories at the same time
Given my software development background and the industry experience I have; I decided to classify programmers. Think of this as a taxonomy, I plan to grow this list as time progresses. A programmer could fall into several categories at the same time
- The Post-it Programmer :- Usually arrogant programmer who believes that he/she was not created to write certain programs or to do lowly jobs like testing or writing test cases. Does a good job like post-it notes, but cannot be used for anything else.
- The Erratic Programmer :- No matter what level experience he/she has, they will always write buggy code.
- The Pretending Programmer :- Pretends to work and thinks that he/she has achieved a lot, but in reality the work done is zero.
- The Cautious Programmer :- Will take forever to think about the program and discuss it forever, but will never make it into useful working code.
- The Cribbing Programmer :- Believes that every one else has better work to do than what he/she does. Such programmers always complain and are never happy with anything
- The Lazy Programmer :- Will waste away time until he/she can. Then at some point realize that wasting time is no longer feasible and starts working
To the professional
I purchased a book that addresses the professional as audience of the book. The solutions and the Instructors Manual is available only to professors and teachers. The question is -- why do the smart people get solutions. I can understand the students not getting the solutions, but why do the professors need it? Are they not already smart to figure out the solutions by themselves?
I purchased a book that addresses the professional as audience of the book. The solutions and the Instructors Manual is available only to professors and teachers. The question is -- why do the smart people get solutions. I can understand the students not getting the solutions, but why do the professors need it? Are they not already smart to figure out the solutions by themselves?
Subscribe to:
Posts (Atom)
Ranking and Unranking permutations
I've been a big fan of Skiena's Algorithm Design Manual , I recently found my first edition of the book (although I own the third ed...
-
I've been a big fan of Skiena's Algorithm Design Manual , I recently found my first edition of the book (although I own the third ed...
-
The book is almost out there . There is code and selected solutions as well. The book is supposed to be in full colour from what I heard....
-
(Photo from http://content-usa.cricinfo.com/indvaus2008/content/current/player/28114.html) Dravid's dismal form continues in test crick...