Comments on Big-Oh (O) from CLRS

Section 3.1 of CLRS (Cormen, Leiserson, Rivest, Stein) discuss the Big-Oh notation O. The linear function an + b is O(n²), which is easily verified by taking c = a + |b|. cg(n) is a²n + ba + |b|b + |b|an. At the first glance this seems true if a + b >= n, since O is the worst case, we can use this. In addition, a = b = sqrt(n) also help in making the function O(n²). Please see the plots below


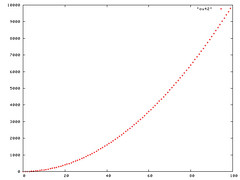
Figure 1: Plot of n²

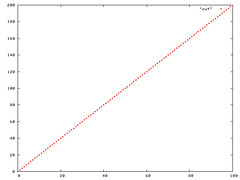
Figure 2: Plot of a = 1,b = n

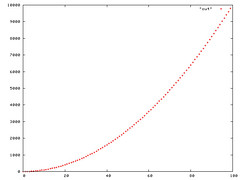
Figure 3: Plot of a = n,b = 1

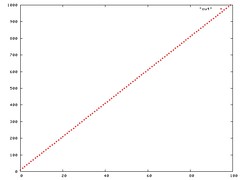
Figure 4: Plot of a = sqrt(n),b = sqrt(n)

Figure 5:Plot of a = 1,b = 1

I think it is non-trivial to suggest find out that the function is indeed
O(n²). Comments please!